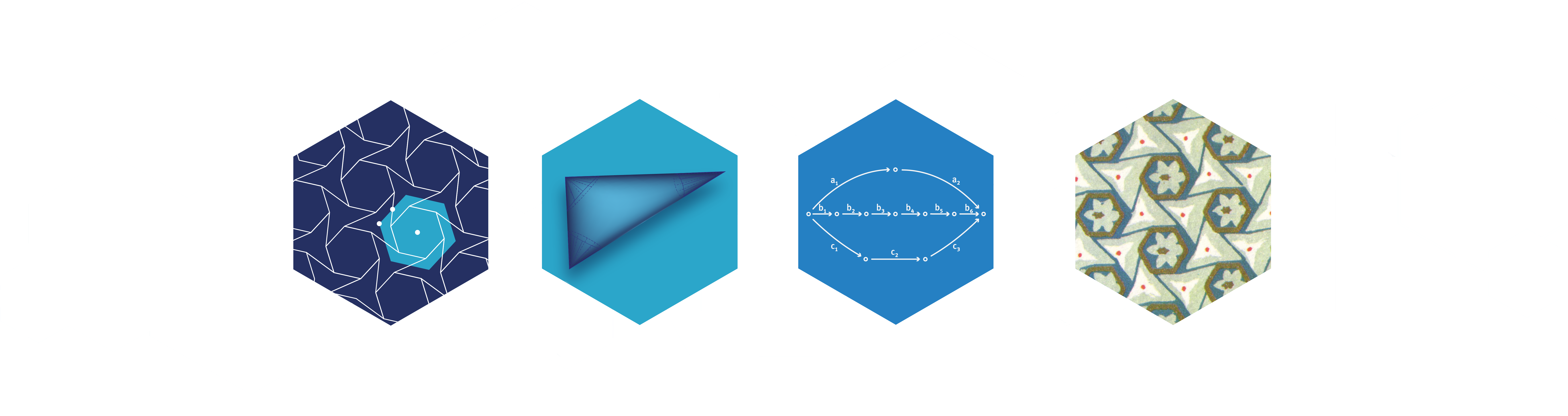
The picture on the right shows a medieval wallpaper pattern from the Alhambra palace in Granada. Its characteristic feature is a high rotational and translational symmetry. On the left one finds an undecorated version of this wallpaper design, which provides a periodic tessellation of the plane. As one can see, it is invariant under rotations by 60, 120 and 180 degrees respectively. These rotations have their centres marked by white dots, and they generate a discrete subgroup of the group of isometries of the Euclidean plane. Different pictures can lead to the same group and it is a classical result that there are precisely 17 nonisomorphic wallpaper groups. Wallpaper groups are examples of integral structures. The quotients of the plane modulo such groups are flat compact surface orbifolds, as shown on the second picture from the left.

If a wallpaper group is generated by rotations, the corresponding orbifold surface inherits the complex structure of the plane. In algebraic language it is a weighted projective line of tubular type. Moreover, the category of coherent sheaves on a weighted projective line admits a tilting object, whose endomorphism algebra is a canonical algebra in the sense of Ringel. The shape of the corresponding quiver can be read off from the orders of the generating rotations, as it is shown on the second picture from the right.

A theorem of Geigle and Lenzing establishes a derived equivalence between the geometric category of coherent sheaves on the orbifold and the module category of the tilted algebra. It signifies the kind of intrinsic and intimate relationship between integral structures, geometry, and representation theory upon which the collaborative research center is predicated.