Integral Structures in Geometry and Representation Theory

Paderborn, 9-13 September 2024

This kick-off conference will encompass the entire research profile of CRC-TRR 358 of Bielefeld and Paderborn University. The format will consist of two plenary lectures every day before lunch. In the afternoon, we will run six parallel sessions.

The conference is organised by Claudia Alfes, Igor Burban, Kai-Uwe Bux, Charles Vial and Tobias Weich.

The registration is open until 15 July 2024.

Plenary speakers

Emanuele Macrì (Orsay)
Gunter Malle (Kaiserslautern)
Yves Meyer (Paris-Saclay)		 Amnon Neeman (Milan)
Hee Oh (Yale)
Alexander Polishchuk (Oregon)
Dipendra Prasad (Mumbai)		 Maryna Viazovska (Lausanne)
Anna Wienhard (MPI-MiS Leipzig)
Efim Zelmanov (SUSTech)

Sessions

  • Aspects of aperiodic order
  • Experimental methods in algebra, geometry and number theory
  • Geometry and analysis of locally symmetric spaces
  • Geometry and arithmetic of moduli spaces
  • Groups and geometry
  • Tame categories, geometric models, and homological mirror symmetry

    • Sponsors

    TRR 358 DFG Uni Bielefeld Uni Paderborn

    Contact

    If you have any questions, please contact Elena Tielker: coordinator_trr358@math.uni-bielefeld.de.

    Programme

    Schedule

    Monday Tuesday
    8.15 – 9.00 Registration
    9.00 – 9.15 Opening
    9.15 – 10.15 Plenary talk
    10.15 – 11.00 Coffee break
    11.00 – 12.00 Plenary talk
    12.00 – 14.00 Lunch break
    14.00 – 16.00 Sessions
    16.00 – 16.30 Coffee break
    16.30 – 18.00 Sessions
     
    Thursday Friday
     
     
    9.15 – 10.15 Plenary talk
    10.15 – 11.00 Coffee break
    11.00 – 12.00 Plenary talk
    12.00 – 14.00 Lunch break
    14.00 – 16.00 Sessions
    16.00 – 16.30 Coffee break
    16.30 – 18.00 Sessions
     
    19.00 Dinner
    Wednesday
     
     
    9.15 – 10.15 Plenary talk
    10.15 – 11.00 Coffee break
    11.00 – 12.00 Plenary talk
    12.00 – 14.00 Lunch break
     
    15.00 Social programme
     

    Sessions

    Aspects of aperiodic order

    Speakers:
  • Maria Isabel Cortez (Pontificia Universidad Católica de Chile)
  • Johannes Kellendonk (Claude Bernard University Lyon 1)
  • David Damanik (Rice University)

    • Participants:
  • Ruiwen Dong (Saarland University)
  • Franz Gähler (Bielefeld University)
  • Markus Kirschmer (Paderborn University)
  • Simon Machado (ETH Zurich)
  • Neil Manibo (Bielefeld University)
  • Timo Spindeler (Bielefeld University)

    • Organisers: Michael Baake, Franz Gähler
    You can register here.

    Experimental methods in algebra, geometry and number theory

    Speakers:
  • Daniele Agostini (Universität Tübingen)
  • Marie-Charlotte Brandenburg (KTH Royal Institute of Technology)
  • Bettina Eick (Technischen Universität Braunschweig)
  • Giles Gardam (Universität Bonn)
  • Yang-Hui He (University of London)
  • Steffen Müller (University of Groningen)
  • Eamonn O'Brien (University of Auckland)
  • Anna-Laura Sattelberger (KTH Royal Institute of Technology)
  • Emre Sertöz (Leiden University)
  • Sara Veneziale (Imperial College London)
  • Nelly Villamizar (Swansea University)
  • Christian Wuthrich (University of Nottingham)

    • Participants:
  • Ana Botero (Bielefeld University)
  • Lars Bügemannskemper (Bielefeld University)
  • Martina Conte (Heinrich-Heine-Universität Düsseldorf)
  • Sebastian Degen (Bielefeld University)
  • Sabyasachi Dhar (IIT Kanpur)
  • Bettina Eick (TU Braunschweig)
  • Óscar Fernández Ayala (TU Braunschweig)
  • Fabian Gundlach (Paderborn University)
  • Lukas Kühne (Bielefeld University)
  • Elyasheev Leibtag (weizmann institute of science)
  • Keivan Mallahi-Karai (Constructor University)
  • Leonie Mühlherr (Bielefeld University)
  • Nicolas Potthast (Paderborn University)
  • Praful Rahangdale (Paderborn University)
  • Daniele Turchetti (Durham University)
  • Eduardo Vital (Bielefeld University)
  • Christopher Voll (Bielefeld University)

    • Provisional schedule:
    Monday Tuesday Thursday Friday
    14.00 – 15.00 Bettina Eick Marie-Charlotte Brandenburg Anna-Laura Sattelberger Steffen Müller
    15.00 – 16.00 Giles Gardam Sara Veneziale Daniele Agostini Emre Sertöz
    16.00 – 16.30 Coffee break Coffee break
    16.30 – 17.30 Eamonn O’Brien Yang-Hui He Nelly Villamizar Christian Wuthrich

    Organisers: Ana Botero, Lukas Kühne, Christopher Voll
    You can register here.

    Geometry and analysis of locally symmetric spaces

    Speakers:
  • Jean Philippe Anker (Université d’Orléans)
  • Claire Burrin (Universität Zürich)
  • Benjamin Delarue (Universität Paderborn)
  • Manfred Einsiedler (ETH Zurich)
  • William Hide (Durham University)
  • Min Lee (University of Bristol)
  • Christopher Lutsko (Universität Zürich)
  • Jens Marklof (University of Bristol)
  • Simon Marshall (University of Wisconsin-Madison)
  • Jasmin Matz (University of Copenhagen)
  • Beatrice Pozzetti (Heidelberg Universität)
  • Uri Shapira (Technion, Israel Institute of Technology)

    • Participants:
  • Claudia Alfes (Bielefeld University)
  • Christian Arends (Aarhus University)
  • Edgar Assing (University of Bonn)
  • Valentin Blomer (University of Bonn)
  • Gabriele Bogo (Bielefeld University)
  • Dominik Brennecken (Paderborn University)
  • Félicien Comtat (Bonn University)
  • Colin Davalo (Universität Heidelberg)
  • Sabyasachi Dhar (IIT Kanpur)
  • Sami Douba (Institut des Hautes Études Scientifiques)
  • Nihar Gargava (IRMA Strasbourg)
  • Giacomo Gavelli (University of Tübingen)
  • Segev Gonen Cohen (ETH Zurich)
  • Jana Göken (University of Bremen)
  • Maiken Gravgaard (Aarhus University)
  • Anna Guntermann (Bielefeld University)
  • Malek Hanounah (Greifswald)
  • Michael Heins (JMU Würzburg)
  • Joachim Hilgert (Paderborn University)
  • Daniel Kahl (Paderborn University)
  • Paul Kiefer (Bielefeld University)
  • Lukas Langen (Universität Paderborn)
  • Effie Papageorgiou (Paderborn University)
  • Carsten Peterson (Paderborn University)
  • Margit Rösler (Paderborn University)
  • Rudolf Scharlau (TU Dortmund)
  • Marc Technau (Paderborn University)
  • Niclas Technau (University of Bonn)
  • Robin van Haastrecht (Gothenburg University/Chalmers)
  • Tobias Weich (Paderborn University)
  • Lasse Wolf (Paderborn University)
  • Hong-Wei Zhang (Paderborn University)

    • Provisional schedule:
    Monday Tuesday Thursday Friday
    14.00 – 15.00 Jean Philippe Anker Jens Marklof Claire Burrin Jasmin Matz (Zoom)
    15.00 – 16.00 Min Lee Manfred Einsiedler Christopher Lutsko Simon Marshall
    16.00 – 16.30 Coffee break Coffee break
    16.30 – 17.30 Benjamin Delarue Uri Shapira William Hide
    17.30 – 18.30 Beatrice Pozzetti

    Organisers: Claudia Alfes, Valentin Blomer, Tobias Weich
    You can register here.

    Geometry and arithmetic of moduli spaces

    Speakers:
  • Raphaël Beuzart-Plessis (CNRS/Aix-Marseille Université)
  • Carel Faber (Utrecht University)
  • Laurent Fargues (CNRS/Institut de Mathématiques de Jussieu)
  • Frank Gounelas (Georg-August-Universität Göttingen)
  • Eugen Hellmann (Universität Münster)
  • Bruno Klingler (HU Berlin)
  • Laura Pertusi (Università degli Studi di Milano)
  • Eva Viehmann (Universität Münster)
  • Ziquan Yang (University of Wisconsin)
  • Wei Zhang (MIT)

    • Participants:
  • Sanskar Agrawal (Indian Institute of Science Education and Research (IISER))
  • Abhijit Aryampilly Jayanthan (Paderborn University)
  • Ignacio Barros (Universiteit Antwerpen)
  • Erick Miguel Diaz Lopez (University of Miami)
  • Salvatore Floccari (Bielefeld University)
  • Shi He (University of Antwerp)
  • Claudius Heyer (Paderborn University)
  • Manuel Hoff (Bielefeld University)
  • Carlo Kaul (Paderborn University)
  • Johannes Krah (Bielefeld University)
  • Alfio Fabio La Rosa (University of Luxembourg)
  • Georg Linden (University of Duisburg-Essen)
  • Weixiao Lu (MIT)
  • Pablo Magni (Bielefeld University)
  • Luigi Martinelli (Bielefeld University)
  • Carl Mazzanti (Bielefeld University)
  • Howard Nuer (Technion, Israel Institute of Technology)
  • Gianni Petrella (University of Luxembourg)
  • Franco Rota (University of Glasgow)
  • Béranger Seguin (Paderborn University)
  • Luca Speciale (Paderborn University)
  • Sören Sprehe (Bielefeld University)
  • Charles Vial (Bielefeld University)
  • Eduardo Vital (Bielefeld University)
  • Xiaoyu Zhang (Universität Duisburg-Essen)
  • Yushu Zhu (Sorbonne université)
  • Haitao Zou (Bielefeld University)

    • Organisers: Ignacio Barros, Eike Lau, Michael Spieß, Charles Vial
    You can register here.

    Groups and geometry

    Speakers:
  • Sebastian Bischof (Paderborn University)
  • Sira Busch (University of Münster)
  • Maria Cumplido (Universidad de Sevilla)
  • Dawid Kielak (University of Oxford)
  • Jon McCammond (UC Santa Barbara)
  • Ismael Morales (University of Oxford)
  • Bernhard M. Mühlherr (Justig-Liebig-Universität Gießen)
  • Luis Paris (Université de Bourgogne)
  • Bertrand Remy (ENS de Lyon)
  • Sarah Rees (Newcastle University)
  • Damiano Rossi (RPTU Kaiserslautern-Landau)
  • Mireille Soergel (MPI-MiS Leipzig)
  • Katrin Tent (Universität Münster)
  • Stefan Witzel (Justig-Liebig-Universität Gießen)

    • Participants:
  • Barbara Baumeister (Bielefeld University)
  • Jean-Baptiste Bellynck (Ludwig-Maximilians-Universität München)
  • Lennart Berg (JLU Gießen)
  • Rekha Biswal (National Institute of Science Education and Research, Bhubaneswar, India)
  • Lars Bügemannskemper (Bielefeld University)
  • Kai-Uwe Bux (Bielefeld University)
  • Ilaria Castellano (Bielefeld University)
  • Dorian Chanfi (Justus-Liebig-Universität Gießen)
  • Isobel Davies (Otto-von-Guericke-Universität Magdeburg)
  • Christian De Nicola Larsen (UNSW Sydney)
  • Jari Desmet (Ghent University)
  • Olasupo Felemu (Adekunle Ajasin University Akungba Akoko Ondo State Nigeria )
  • Max Gheorghiu (University of British Columbia)
  • Helge Glöckner (Paderborn University)
  • Doris Grothusmann (Heinrich-Heine-Universität Düsseldorf)
  • Elisa Hartmann (Bielefeld University)
  • Steffen Kionke (FernUniversität in Hagen)
  • Lukas Klawuhn (Paderborn University)
  • Adam Klukowski (University of Oxford)
  • Waltraud Lederle (TU Dresden)
  • Antonio Lopez Neumann (IMPAN)
  • Bianca Marchionna (Bielefeld University)
  • Philip Möller (Hhu Düsseldorf)
  • Thiziri Moulla (Université de Montpellier)
  • Zwelethemba Mpono (University of South Africa)
  • Dr. Abhishek Mukherjee (The University of Burdwan)
  • Georges Neaime (Bielefeld University)
  • Sangrok Oh (University of the Basque Country)
  • Effie Papageorgiou (Paderborn University)
  • Carsten Peterson (Paderborn University)
  • Moritz Petschick (Bielefeld University)
  • Kaitlin Ragosta (Brandeis)
  • Andriy Regeta (University of Jena)
  • Tomas Reunbrouck (Bielefeld University)
  • Bhola Nath Saha (Indian Institute of Technology Kanpur)
  • Paul Hannes Schneider (Bielefeld University)
  • Patrick Serwene (TU Dresden)
  • Ilia Smilga (University of Oxford)
  • Alexander Stolin (Chalmers and University of Göteborg, Sweden )
  • Inga Valentiner-Branth (Ghent University)
  • Lukas Vandeputte (KU Leuven)
  • Noam von Rotberg (Bielefeld University)
  • Patrick Wegener (Leibniz Universität Hannover)
  • Charlene Weiß (Paderborn University)
  • Torben Wiedemann (Justus-Liebig-Universität Gießen)
  • Kevin Zwart (Radboud University Nijmegen)

    • Organisers: Kai-Uwe Bux, Barbara Baumeister
    You can register here.

    Tame categories, geometric models, and homological mirror symmetry

    Speakers:
  • Karin Baur (Ruhr-Universität Bochum)
  • Raphael Bennett-Tennenhaus (Aarhus University)
  • Raf Bocklandt (University of Amsterdam)
  • Cheol-Hyun Cho (Seoul National University)
  • Merlin Christ (Institut de Mathématiques de Jussieu)
  • Christoph Geiß (Universidad Nacional Autónoma de México)
  • Daniel Labardini-Fragoso (Universidad Nacional Autónoma de México)
  • Sebastian Opper (Charles University)
  • Pierre-Guy Plamondon (Université de Versailles Saint-Quentin-en-Yvelines)
  • Sibylle Schroll (Universität zu Köln)
  • Jasper van den Kreeke (University of Amsterdam)
  • Alexandra Zvonareva (Czech Academy of Science)

    • Participants:
  • Severin Barmeier (University of Cologne)
  • Shomrik Bhattacharya (University of Southern Denmark)
  • Pierre Bodin (Université de Versailles Saint-Quentin, Université de Sherbrooke)
  • Igor Burban (Paderborn University)
  • William Crawley-Boevey (Bielefeld University)
  • Sebastian Eckert (Bielefeld University)
  • Wassilij Gnedin (Paderborn University)
  • Juan Omar Gomez (Bielefeld University)
  • Aakash Gopinath (University of Amsterdam)
  • Wenjun Huang (University of Amsterdam)
  • Shin Komatsu (University of Amsterdam)
  • Henning Krause (Bielefeld University)
  • Janina Letz (Bielefeld University)
  • Stepan Maximov (Paderborn University)
  • Daniel Perniok (Paderborn University)
  • Kyungmin Rho (Paderborn University)
  • Giovanni Rossanigo (Università degli Studi di Milano)
  • Julia Sauter (Bielefeld University)
  • Charly Schwabe (Paderborn University)
  • Marc Stephan (Bielefeld University)

    • Organisers: Igor Burban, William Crawley-Boevey, Henning Krause, Kyungmin Rho
    You can register here.

    Social programme


    Details regarding meeting points and other logistical information will be provided on this website shortly before the conference begins. Additionally, all relevant information will be displayed at the conference venue.


    Bicycle tour

    We explore the Paderborn area with rental bikes organized by us. The bike tour takes about three hours.

    Guided tour

    In a 90-minute city tour, we explore the highlights of Paderborn's beautiful city center.

    Heinz-Nixdorf museum

    https://www.hnf.de/en/home.html
    We visit the Heinz Nixdorf Museumsforum (HNF), the world's largest computer museum. After a one-hour guided tour, you have the opportunity to explore the exhibition on your own.

    Hike

    Many people don't know it, but Germany's shortest river, the Pader, has its source in Paderborn. As part of a 2-3 hour hike, we follow the Pader from its springs to its mouth and then hike back to Paderborn via a circular route.

    Location

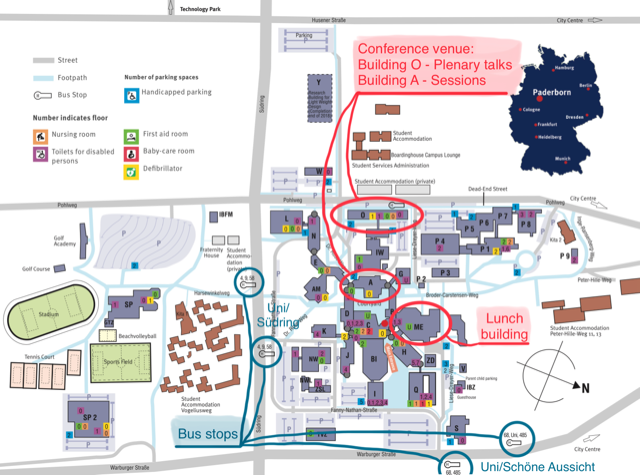
    The conference will take place at the main campus of Paderborn University. The plenary talks take place in Building O, in the lecture halls O1 and O2, the sessions in the afternoon are held in Buildings O and A. The coffee breaks take place in Building O, in rooms O1.224 and O1.258.
    The registration takes place in the foyer O1 in Building O.

    How to get there

    Bus:
    It is possible to reach the campus from the city center by foot in roughly 30 minutes or alternatively by bus in about 15 minutes. Tickets can be purchased
  • on the bus (only cash)
  • at many busstations (including main station),
  • online at shop.padersprinter.de (creditcard payment).
    • The bus stops close to the campus are "Uni/Südring" and "Uni/Schöne Aussicht" and are indicated in the map below.

    Train stations and airports:
    The nearest train stations are Paderborn Hauptbahnhof (main station) and Paderborn Kasseler Tor (S-Bahn to/from Bielefeld). By air, Paderborn is served by Paderborn-Lippstadt (PAD, 20km, Bus), Hannover (HAJ, 130km, 2h10 direct S-Bahn) and Düsseldorf (DUS, 160km, 2h02 direct S-Bahn). Frankfurt Airport (FRA) is about 3 hours by train and requires at least one connection (in Kassel Wilhelmshöhe or Essen). Amsterdam Schiphol (AMS) is 4h30 by train with at least two connections.

    Accommodations

    A limited number of rooms have been set aside at various hotels for participants. To access these contingents you need to contact the hotels directly by email:
  • Hotel Aspethera (Code: "UNI09092024-TRR358", until 17.6.2024)
  • Welcome Hotel (Code: "TRR 358", until 29.7.2024)
  • IBB Hotel (Code: "TRR 358", until 7.7.2024)
  • B&B Hotel (Code: "TRR 358", until 1.8.2024)
  • ibis Hotel (Link)

    • Child care

    We offer child care for children from the age of one year during the conference from Monday, 9 September, to Friday, 13 September. The children will be supervised in the facility by qualified staff, assisted by Education Studies students.
    If you are interested in this offer, please indicate this when registering.